Ce n'est pas que ce soit très réjouissant quand on connaît la vanité de la spéculation et le désastre écologique qu'il entraîne, mais il faut bien s'intéresser à Bitcoin, ne serait-ce que pour comprendre en quoi consiste concrètement le concept de blockchain dont on nous rebat les oreilles matins et soirs.
Tout le problème pour le développeur, c'est de savoir par quel bout le prendre. C'est que si l'on parle ici de Bitcoin, et non du Bitcoin, c'est bien parce qu'une particularité de la chose, c'est d'être un système avant d'être une cryptomonnaie, que l'on pressent un peu du genre un peu l'oeuf qui fait la poule qui fait l'oeuf, qui plus est. Dès lors, quel est le bon point d'entrée dans ce dernier ?
On trouve pléthore de présentation de Bitcoin sur le Web comme en librairie. Le problème, c'est que leur lecture laisse assez inévitablement le développeur sur le sentiment qu'il n'est pas allé au fond des choses. En fait, pour bien comprendre de quoi il en retourne, l'animal sent bien qu'il faudrait qu'il plonge sa truffe dans les entrailles, manière de dire qu'il faudrait tout simplement prendre un bloc sous sa forme la plus brute, et le disséquer pour comprendre comment il a été produit et inscrit dans la blockchain.
Telle est la démarche adoptée ici. Il s'agit de programmer en Python de quoi désérialiser un bloc existant et valider une transaction qu'il contient. Dans un premier temps, le bloc choisi est le premier bloc, dit "Genesis", car le bon sens impose de partir de celui-là pour comprendre en quoi un bloc consiste. Dans un second temps, le bloc choisi est le 170, car c'est le premier qui contient une transaction véritable - au sens d'un transfert de BTC -, si bien que le bon sens impose de le choisir pour valider une transaction.
Il n'est donc pas question de couvrir le minage, et donc la résolution élégante du problème des généraux byzantins à laquelle est parvenue Satoshi Nakamoto qui constitue la principale innovation de Bitcoin. Encore une fois, l'objectif de cet article reste bien modeste : ce n'est pas de faire comprendre le système Bitcoin, mais de faire comprendre la blockchain de Bitcoin, de la manière la plus efficiente possible pour un développeur.
Avec Bitcoin, le code, c'est la doc
Le premier réflexe à avoir pour se saisir d'une nouvelle technologie est de se mettre en quête de sa spécification. Pour ce qui concerne Bitcoin, le principal document utilisé pour écrire le code décodant le binaire d'un bloc dans le cadre de cet article se trouve ici. Il se présente comme une spécification du protocole Bitcoin.
Que pour comprendre comment est formée une structure de données centrale dans la blockchain, il faille se reporter à un document qui décrit un "protocole" et non un modèle de données en dit déjà long sur la nature de Bitcoin. Commencer l'étude de ce système à partir de la blockchain et non d'un bloc, c'est commettre une faute de goût : dans un système décentralisé, il faut partir de ce que les acteurs s'échangent, c'est-à-dire des blocs, et avant même cela, des transactions, plutôt que de partir du produit de leur action collective, la blockchain en question.
Par ailleurs, les pages de ce Wiki débutent régulièrement par des avertissements dont il ne faut pas négliger la portée. Du genre :
This page describes the behavior of the reference client. The Bitcoin protocol is specified by the behavior of the reference client, not by this page.
This document is for information purposes only. De facto, Bitcoin script is defined by the code run by the network to check the validity of blocks.
Autrement dit, pour ce qui concerne Bitcoin, le code, c'est la doc.
Quel code alors ? A priori celui de Bitcoin Core, qui se présente comme "a direct descendant of the original Bitcoin software client released by Satoshi Nakamoto after he published the famous Bitcoin whitepaper". Le code, qu'il est possible de récupérer sur un Git, comprend de quoi faire fonctionner un full-node et un wallet.
Toutefois, il s'agit d'un code en C++ dans lequel il n'est pas très simple de se plonger. Le principal obstacle, c'est que chercher à comprendre Bitcoin à partir du binaire des premiers blocs de la blockchain, c'est remonter dans le temps, à savoir manipuler des structures et des fonctionnalités qui ont évolué depuis, au fil de l'adoption de BIPS (Bitcoin Improvement Proposals). De ce fait, se référer à ce code contemporain conduit à souvent se demander ce qu'il est pertinent de retenir dans les structures et les fonctionnalités pour manipuler les premiers blocs sans commettre d'anachronisme.
Heureusement, il existe un autre code, accessible sur le site du Satoshi Nakamoto Institute. L'intitulé est peut-être pompeux, mais il faut bien reconnaître que ce site apparaît à la hauteur de ses prétentions, car il réunit nombre de documents et de codes des premiers temps du Bitcoin. En particulier, l'on y trouve le code de la version 0.1.0 de Bitcoin.
En plus de remonter à l'époque des premiers blocs, ce code est bien plus léger que le code contemporain de Bitcoin Core. C'est à ce double titre qu'il constitue la référence recommandée.
En même temps qu'il convient de recommander de se plonger dans ce code, il convient de recommander de se plonger dans la lecture des échanges dans les forums entre Satoshi Nakamoto et ceux auprès desquels il a entrepris de promouvoir Bitcoin. C'est une précieuse source d'informations pour comprendre en quoi consiste Bitcoin, et pourquoi il se présente sous la forme qu'on lui connaît. En un mot, c'est une sorte de manuel de survie pour qui prétend explorer Bitcoin.
Ainsi, comme dit plus tôt : le code, c'est la doc. La lecture des échanges montre que cela a toujours été le cas, et ceux qui pointent l'existence du fameux papier écrit par Satoshi Nakamoto, "Bitcoin: A Peer-to-Peer Electronic Cash System", comme une référence en seront pour leurs frais s'ils s'en contentent pour comprendre ce qu'est Bitcoin dans les détails avant de mettre les mains dans le cambouis.
Pour preuve, ce fil de discussion. Après avoir lu le document, Hal Finney - qui s'imposera comme le principal contributeur à Bitcoin - pose une série de questions à Satoshi Nakamoto, qu'il termine par :
You mentioned that you are working on an implementation, but I think a more formal, text description of the system would be a helpful next step.
A quoi Satoshi Nakamoto répond :
I actually did this kind of backwards. I had to write all the code before I could convince myself that I could solve every problem, then I wrote the paper.
Et plus tard :
The functional details are not covered in the paper, but the sourcecode is coming soon.
Et encore plus tard, au détour d'un échange qui déborde le seul sujet technique, Satoshi Nakamoto en vient à dire :
I'm better with code than with words though.
Dès lors, qui lit le code la version 0.1.0 comprend un peu mieux pourquoi la réalité de Bitcoin est bien plus complexe que ce que la lecture du papier laisse à penser. Par exemple, il y a tout un monde entre la "signature d'une transaction" et la manière dont elle s'opère concrètement, par input, en comprenant par ailleurs une étape dont le sens n'a rien d'évident, pour autant qu'elle en ait eu vraiment. Dans script.cpp, le code qui procède à la vérification d'une signature comprend :
// Drop the signature, since there's no way for a signature to sign itself scriptCode.FindAndDelete(CScript(vchSig));
Cette étape semble oubliée. Ainsi, elle n'apparaît pas (ou plus ?) dans le schéma qui décrit la validation d'une signature dans la description protocole contemporain. Scorie résultant d'expérimentations abandonnées ? Anticipation véritable d'une fonctionnalité qui n'a jamais été implementée ? Personne n'a pour l'heure répondu à cette question...
Cela tient au fait que Satoshi Nakamoto a conçu un système qu'il a voulu évolutif en tenant compte du fait que dès le départ, certaines choses seraient irrémédiablement gravées dans le marbre. Or ce qu'il avait en tête allait bien au-delà de simplement permettre à Alice d'envoyer 10 de ses 50 BTC à Bob et de garder le reste, comme c'est présenté à l'envi dans la littérature. Ce message est édifiant à cet égard. On lit notamment :
The nature of Bitcoin is such that once version 0.1 was released, the core design was set in stone for the rest of its lifetime. Because of that, I wanted to design it to support every possible transaction type I could think of.
[...]
The design supports a tremendous variety of possible transaction types that I designed years ago. Escrow transactions, bonded contracts, third party arbitration, multi-party signature, etc. If Bitcoin catches on in a big way, these are things we'll want to explore in the future, but they all had to be designed at the beginning to make sure they would be possible later.
Il n'en reste pas moins que quelques références sont fort utiles. En voici deux :
- Mastering Bitcoin, de Andreas M. Antonopoulos, publié chez O'Reilly en 2014 ;
- Programming Bitcoin, de Jimmy Song, publié chez O'Reilly en 2019.
Somme toute, s'il devait n'en lire qu'un, c'est ce dernier livre qu'un développeur devrait lire, car son sujet est celui qui le préoccupera comme il a préoccupé l'auteur de cet article : "Learn how to program Bitcoin from scratch"...
Le code
Ca ne rigole pas sur ce blog : d'abord on dégaine son code, ensuite on discute. D'ailleurs, toutes les explications qui suivent constituent une sorte de long commentaire de code, qu'il convient donc de parcourir parallèlement. Cliquez ici pour télécharger une archive qui contient le code Python suivant :
| downloadBlocks.py | Point de départ qui consiste simplement à télécharger un bloc ou une suite de blocs en JSON et en binaire depuis Blockchain explorer, et à sauvegarder tout cela dans des fichiers pour les manipuler hors ligne ensuite. |
| checkBlockchain.py | Désérialisation d'un bloc ou d'une série de blocs à partir du binaire, sous la forme d'objets, suivie de la vérification de l'exactitude de cette désérialisation par recoupement avec le JSON, et du dump du contenu sous forme de texte lisible. Au passage, le calcul du hash du header d'un bloc et celui de la racine du Merkle tree des transactions qu'il contient sont effectués et vérifiés, ici encore par recoupement avec le JSON. |
| btc/objects.py | Factorisation des classes des objets définis lors dans le checkBlockchain.py, pour les programmes qui suivent. |
| btc/tools.py | Factorisation des outils définis lors dans checkBlockchain.py, pour les programmes qui suivent. |
| validateTransaction.py | Validation de la fameuse transaction de 10 BTC de Satoshi Nakamoto à Hal Finney qui figure dans le bloc 170. Enfin, l'extraction des éléments qui permettent cette validation par OpenSSL, à savoir : le hash (au format binaire) de type SIGHASH_ALL de la transaction 1 du bloc 170, la signature (au format DER) tirée du scriptSig de l'input 0 de cette transaction, la clé publique (au format DER) tirée du scriptPubKey de l'output 0 de la transaction 0 du bloc 9 sur laquelle renvoie l'input évoquée. |
| mineBlock.py | Amorce du minage du bloc 170. C'est hors-sujet dans le cadre de cet article, et c'est par ailleurs inachevé, mais cela peut présenter un intérêt pour le lecteur qui voudrait pousser les feux. Il s'agit simplement de recréer le bloc 170 from scratch, aux valeurs des champs ajustées lors de la recherche du hash près, et de vérifier que le bloc est bon en comparant son hash à celui du bloc 170 réel. |
Ce code n'est absolument pas optimisé, seule compte sa lisibilité.
Dissection du bloc Genesis
Sachant que l'on ne peut pas faire plus bas-niveau, le point de départ est le binaire du bloc 0 de la blockchain du Bitcoin, dit "Genesis". Ce binaire peut être obtenu sur un de ces sites qui proposent d'explorer le contenu de la blockchain en exposant divers services. En l'espèce via cette requête à un service de BlockChain.com... :
https://blockchain.info/rawblock/000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f?format=hex
...qui renvoie la représentation sous forme de texte de la valeur en hexadécimale des octets qui composent le binaire :
0100000000000000000000000000000000000000000000000000000000000000000000003ba3edfd7a7b12b27ac72c3e67768f617fc81bc3888a51323a9fb8aa4b1e5e4a29ab5f49ffff001d1dac2b7c0101000000010000000000000000000000000000000000000000000000000000000000000000ffffffff4d04ffff001d0104455468652054696d65732030332f4a616e2f32303039204368616e63656c6c6f72206f6e206272696e6b206f66207365636f6e64206261696c6f757420666f722062616e6b73ffffffff0100f2052a01000000434104678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5fac00000000
La lecture de la description des structures dans la spécification du protocole Bitcoin permet de déchiffrer ce binaire manuellement pour se faire une première idée du contenu d'un bloc :
| ----- Header (début) ----- |
|
Version
01 00 00 00
|
|
Double SHA-256 du bloc précédent
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
|
|
Racine du Merkle tree des transactions
3B A3 ED FD 7A 7B 12 B2 7A C7 2C 3E 67 76 8F 61 7F C8 1B C3 88 8A 51 32 3A 9F B8 AA 4B 1E 5E 4A
|
|
Timestamp
29 AB 5F 49 (3 janvier 2009 18:15:05)
|
|
Bits
FF FF 00 1D (Difficulté : 000000001d00ffff000000000000000000000000000000000000000000000000)
|
|
Nonce
1D AC 2B 7C (2083236893)
|
| ----- Header (fin) ----- |
|
Nombre de transactions (entier de taille variable)
01
|
| ----- Transaction (début) ----- |
|
Version
01 00 00 00
|
|
Présence de témoins ? (SegWit n'apparaît qu'à partir du bloc 481824)
(non car la séquence de deux octets n'est pas 00 01)
|
|
Nombre d'inputs (entier de taille variable)
01
|
| ----- Input (début) ----- |
|
Hash de la transaction antérieure
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
|
|
Indice de l'output dans la transaction antérieure
FF FF FF FF
|
|
Longueur de scriptSig (entier de taille variable)
4D (77 octets)
|
|
scriptSig
04 FF FF 00 1D 01 04 45 54 68 65 20 54 69 6D 65 73 20 30 33 2F 4A 61 6E 2F 32 30 30 39 20 43 68 61 6E 63 65 6C 6C 6F 72 20 6F 6E 20 62 72 69 6E 6B 20 6F 66 20 73 65 63 6F 6E 64 20 62 61 69 6C 6F 75 74 20 66 6F 72 20 62 61 6E 6B 73
|
|
Séquence
FF FF FF FF
|
| ----- Input (fin) ----- |
|
Nombre d'outputs (entier de taille variable)
01
|
| ----- Output (début) ----- |
|
Valeur en Satoshis (nombre de BTX / 10^8)
00 F2 05 2A 01 00 00 00 (5 milliards de Satoshis = 50 BTC)
|
|
Longueur de scriptPubKey (entier de taille variable)
43 (67 octets)
|
|
scriptPubKey
41 04 67 8A FD B0 FE 55 48 27 19 67 F1 A6 71 30 B7 10 5C D6 A8 28 E0 39 09 A6 79 62 E0 EA 1F 61 DE B6 49 F6 BC 3F 4C EF 38 C4 F3 55 04 E5 1E C1 12 DE 5C 38 4D F7 BA 0B 8D 57 8A 4C 70 2B 6B F1 1D 5F AC
|
|
----- Output (fin) ----- ----- Transaction (fin) ----- |
|
Pas de verrouillage / Numéro du bloc / Date heure de verrouillage
00 00 00 00 (pas de verrouillage)
|
D'emblée, deux constats s'imposent :
- Tout d'abord, il est largement fait usage du little endian. En fait, tout est en little endian, sauf les scripts.
-
Ensuite, tout est fait pour économiser des octets. Ainsi, le bloc contient plusiers entiers stockés sous forme de séries d'octets à taille variable (1, 3, 5 ou 9 octets) par application de l'algorithme suivant :
def variantToBytes (n): data = bytearray () if n < 0xfd: # N < 0xfd : N sur 1 octet size = 1 elif n < 0xffff: # 0xfd <= N < 0xffff : 0xfd puis N sur 2 octets size = 2 data.append (0xfd) elif n < 0xffffffff: # 0xffff <= N < 0xffffffff : 0xfe puis N sur 4 octets size = 4 data.append (0xfe) else: # 0xffffffff <= N : 0xff puis N sur 8 octets size = 8 data.append (0xff) data.extend (n.to_bytes (size, byteorder='little')) return data, len (data)
Pour l'anecdote, la taille des données est devenue un enjeu crucial pour la communauté Bitcoin, au point qu'il a pu radicalement la diviser. Ainsi, l'introduction de SegWit pour notamment réduire le nombre d'octets pris en compte dans le calcul du hash d'une transaction a conduit certains mineurs à faire bande à part en créant Bitcoin Cash. Cette histoire savoureuse est notamment narrée dans un article de The Verge.
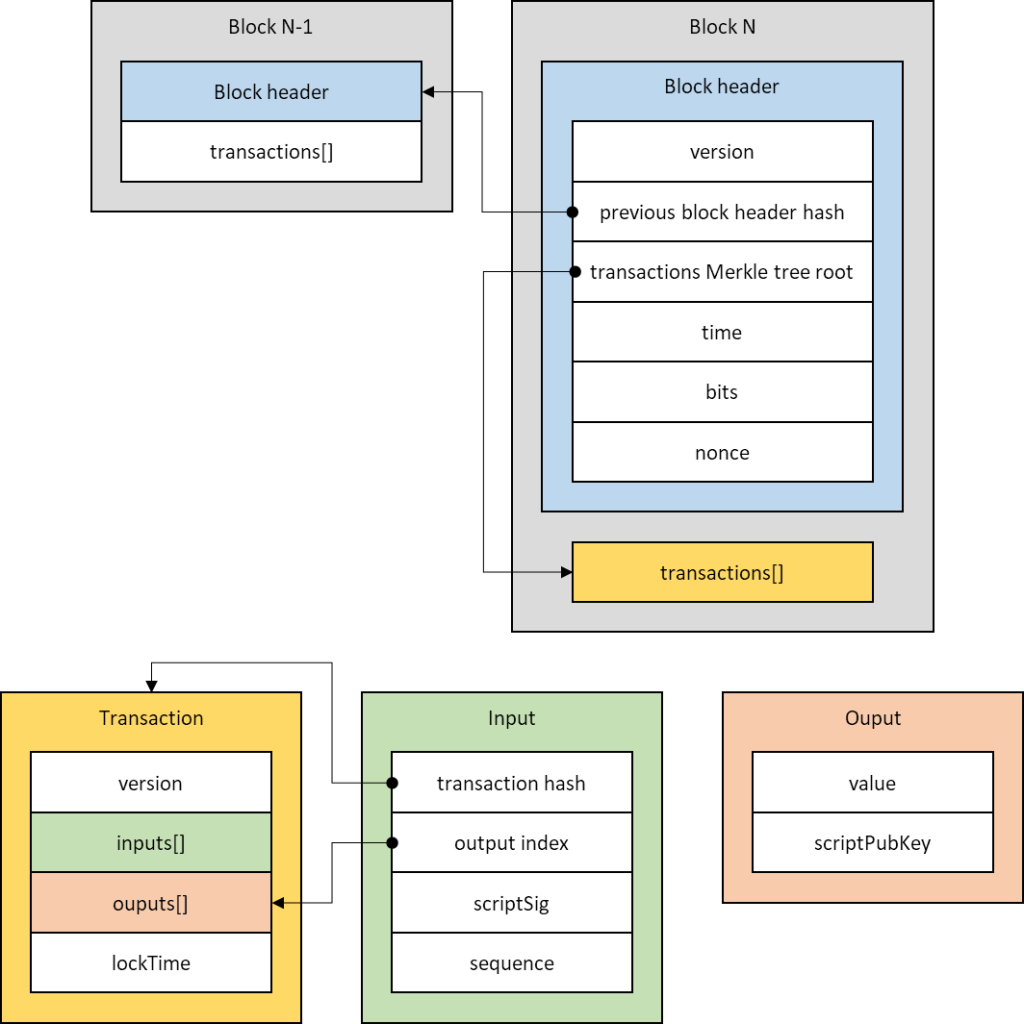
Un bloc contient des transactions. Une transaction comporte un certain nombre d'inputs qui sont transformées en un certain nombre d'outputs. Pour savoir combien de BTC sont en circulation à un instant donné, il faut cumuler les BTC des outputs des transactions du bloc courant et ceux des outputs des transactions des blocs antérieurs qui ne sont pas utilisées comme inputs dans les transactions du bloc courant. Ces outputs, qui correspondent à des BTC qui ne sont donc pas encore dépensés, sont désignées comme les UTXO (Unspent Transaction Output).
Une transaction est identifiée par son hash, un double SHA-256 de ses octets. Toutefois, ce hash ne figure nulle part dans les octets du bloc. Le seul hash relatif aux transactions que l'on y trouve, c'est le hash qui constitue la racine du Merkle tree des transactions du bloc.
Au-delà de ce hash relatif aux transactions du bloc, le bloc contient bien des hashes de transactions. Toutefois, il s'agit de transactions antérieures - ie : elles résident des blocs antérieurs - auxquelles les inputs des transactions du bloc font référence.
En effet, une input d'une transaction correspond toujours une output d'une transaction antérieure. Pour faire le lien, l'input contient le hash de la transaction antérieure et l'indice de l'ouput dans cette transaction.
Toutefois, l'unique input de la première transaction d'un bloc est particulière. Elle est dite "coinbase". Son input ne fait référence à aucune output (-1 donc 0xfffffff) d'aucune transaction antérieure (0 donc un hash de 32 octets 0x00). Son scriptSig doit être interprété comme un paramètre dont la valeur est arbitraire. Par convention, en le décodant comme un script, on y retrouverait notamment la valeur de bits, telle qu'elle figure dans le header du bloc, et un nombre extra nonce incrémenté chaque fois que la valeur de nonce déborde lors du minage.
Il faut utiliser le conditionnel, car si c'est bien ce qui s'observe dans les premiers blocs, comme par exemple dans le Genesis... :
PUSH 4 bytes: ffff001d (rappel de "bits") .... PUSH 1 bytes: 04 (visiblement "extra nonce") . PUSH 69 bytes: 5468652054696d65732030332f4a616e2f32303039204368616e63656c6c6f72206f6e206272696e6b206f66207365636f6e64206261696c6f757420666f722062616e6b73 The Times 03/Jan/2009 Chancellor on brink of second bailout for banks
...ce n'est apparement plus le cas de nos jours. Ainsi, dans le bloc 709703 miné à l'heure où ces lignes sont écrites, le scriptSig décodé comme si c'était un script (*UNKNOWN* signifiant qu'il était impossible de décoder l'opcode 0xfa et donc ce qui suit) donne :
PUSH 3 bytes: 47d40a G.. PUSH 27 bytes: 4d696e656420627920416e74506f6f6c3733363b015f004307c52d Mined by AntPool736;._.C..- *UNKNOWN*: fabe6d6dce946a3115c78ecf3fe707d9eb07e205f324a73cfbcb06dfbe49131caecc5b090200000000000000505c0000662c0200 ..mm..j1....?........$.<.....I....[.........P\..f,..
La coinbase n'a donc pas d'input au sens propre. Elle n'a qu'une output, qui correspond à l'appropriation par le mineur de BTC créés à partir de rien, en récompense de son travail.
Au fait, comment décoder scriptSig et scriptPubKey ainsi que cela vient d'être fait à l'instant ? Il s'agit de scripts destinés à une machine à pile. Un script se présente sous la forme d'une séquence d'opcodes pour empiler / dépiler des données et appeler des fonctions. Une fonction dépile les données qui lui sont passées en paramètres et empile celles qu'elle produit. Scripter pour ce type de machine s'apparente donc à programmer sur une calculatrice en notation polonaise inversée.
Dans le cas présent, les opcodes font tous un octet, sauf ceux qui permettent d'empiler des octets - un tableau vide ; une séquence de 1 à 75 octets ; une séquence de N octets où N est codé sur un, deux ou quatre octets ; l'entier -1 ; l'entier 1 ; les entiers de 2 à 16. Il est donc très simple de décoder un script.
Le décodage de scriptSig donne ainsi :
| 04 | Empiler les 4 octets qui suivent |
| FF FF 00 1D | 4 octets à empiler |
| 01 | Empiler l'octet qui suit |
| 04 | 1 octet à empiler |
| 45 | Empiler les 69 octets qui suivent |
| 54 ... 73 | 69 octets à empiler ("The Times 03/Jan/2009 Chancellor on brink of second bailout for banks") |
Celui de scriptPubKey donne :
| 41 | Empiler les 65 octets qui suivent |
| 04 ... 5F | 65 octets à empiler |
| AC | OP_CHECKSIG |
Le scriptSig de l'input 0 de la coinbase n'est pas le seul endroit où il est possible de stocker des données qui n'ont aucun rapport avec l'échange de BTC, et qui seront préservées, puisque le calcul des hashes en dépend, sur l'exemple de "The Times 03/Jan/2009 Chancellor on brink of second bailout for banks". Cela a donné lieu à des découvertes surprenantes.
Pourquoi extra nonce ?
Comme on le sait, un hash est un nombre de taille prédéterminée calculé à partir de données. Un bon hash doit exhiber certaines qualités, et notamment celles de paraître totalement aléatoire. Ainsi, un algorithme tel que le double SHA-256 utilisé pour calculer le hash du header d'un bloc produit des hashes radicalement différents si le moindre bit est inversé dans le header.
Pour miner un bloc, un mineur doit jouer sur son contenu jusqu'à ce que le hash du bloc soit inférieur ou égal à un nombre de 32 octets, dit target. Ce nombre figure sous forme compacte dans le header : c'est bits. Une formule prédéfinie permet de déduire la valeur de target de celle de bits - après que cette dernière a bien été lue comme un entier sur 32 bits stocké en little endian :
target = bits * 2 ** (8 * (0x1b - 3))
Ce qui revient à décaler bits de 192 bits vers la gauche.
Pour trouver le hash, un mineur doit nécessairement pouvoir modifier le header. Pour cela, il peut jouer sur les valeurs de nonce (4 octets) et de timestamp (4 octets) dans le header, ainsi que sur celle de extra nonce (2 à 100 octets). De fait, extra nonce est logé dans le scriptSig de la première input de la première transaction, si bien que le modifier implique de recalculer le Merkle tree des transactions, donc de modifier le hash qui en est la racine, donc de modifier le header puisque cette racine y est mentionnée.
Dissection du bloc 170
A partir du bloc 0, le Genesis, tous les blocs se ressemblent assez jusqu'au 170, au sens où ils ne contiennent qu'une transaction, laquelle comporte :
-
Une input, dont le scriptSig est :
PUSH (la valeur de "bits" dans le header en little endian, soit 0xffff01d) PUSH ("extra nonce" sur un ou deux octets)Exception faite du bloc Genesis, qui donc rajoute à cela :PUSH "The Times 03/Jan/2009 Chancellor on brink of second bailout for banks"
-
Une ouput de 50 BTC, dont le scriptPubKey est :
PUSH (65 octets) OP_CHECKSIG
S'agissant toujours de la première transaction d'un bloc, c'est une coinbase, ce qui signifie que tous les BTC sont produits à partir de rien et reviennent au mineur du bloc.
Le contenu de scriptSig de l'input a déjà été expliqué. Pour ce qui concerne scriptPubKey de l'output, il s'agit de la seconde partie d'un script dont la première sera constituée par le scriptSig d'une input d'un transaction future, input qui fera référence à l'output. Pour comprendre comment cela fonctionne, il est donc nécessaire de se reporter à une telle transaction. La première se trouve dans le bloc 170.
Le bloc 170 est le premier qui contient deux transactions. La première est sur le modèle des précédentes. La seconde comporte :
-
Une input qui fait référence à l'unique output 0 de 50 BTC de l'unique transaction 0 du bloc 9, dont le scriptSig est :
PUSH (71 octets)
-
Deux outputs, dont les scriptPubKey sont sur le modèle de ceux déjà vus dans les transactions :
-
une output de 10 BTC, dont le scriptPubKey est :
PUSH (65 octets) OP_CHECKSIG
-
une output de 40 BTC, dont le scriptPubKey est :
PUSH (65 octets) OP_CHECKSIG
-
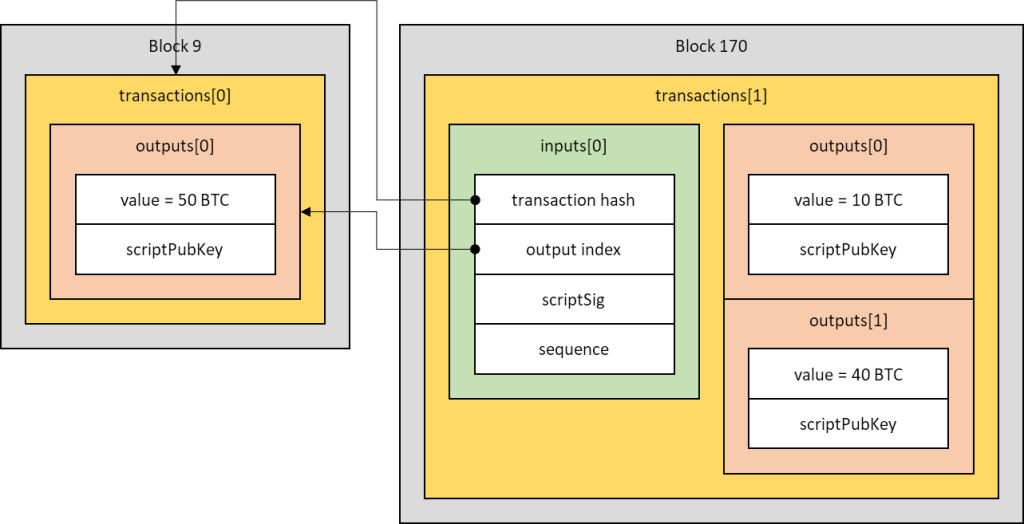
Bref, parce qu'un dessin vaut mieux qu'un long discours :
Validation de la transaction 1 du bloc 170
Comme toute transaction de base qui n'est la première d'un bloc - donc pas la coinbase -, la seconde transaction vise à transférer la propriété de BTC issus d'une transaction d'un bloc antérieur. Les 50 BTC sont répartis en 10 et 40 BTC, mais qui sont donc les propriétaires ? Pour le savoir, il faut dérouler les scripts impliqués dans la transaction.
Pour commencer, le scriptSig de l'input est assemblé avec le scriptPubKey de l'output à laquelle elle fait référence pour former un nouveau script, séparés par un opérateur de séparation :
---- Bloc 170 / Transaction 1 / Input 0 / scriptSig ----- PUSH 304402204e45e16932b8af514961a1d3a1a25fdf3f4f7732e9d624c6c61548ab5fb8cd410220181522ec8eca07de4860a4acdd12909d831cc56cbbac4622082221a8768d1d0901 ---- Séparateur ----- OP_CODESEPARATOR ---- Bloc 9 / Transaction 0 / Output 0 / scriptPubKey ----- PUSH 0411db93e1dcdb8a016b49840f8c53bc1eb68a382e97b1482ecad7b148a6909a5cb2e0eaddfb84ccf9744464f82e160bfa9b8b64f9d4c03f999b8643f656b412a3 OP_CHECKSIG
NB : Ce n'est pas la seule modification survenue depuis, mais il convient de relever que depuis 2010 ce n'est plus le cas. En effet, les scripts ne sont plus concaténés mais exécutés l'un après l'autre pour parer une attaque consistant à utiliser scriptSig pour laisser traîner des données sur la pile afin de corrompre scriptPubKey.
Le script est alors exécuté.
L'opération OP_CHECKSIG est documentée ici, mais une lecture du code de Bitcoin 0.1.0 s'est révélée indispensable pour apporter les précisions qui suivent.
OP_CHECKSIG dépile plusieurs opérandes. Dans l'ordre, et en faisant attention car les nombres sont ici en big endian :
-
(Bloc 9 / Transaction 0 / Output 0 / scriptPubKey) Une clé publique formée par la concaténation de deux nombres x et y de 32 octets en big endian :
x = 11db93e1dcdb8a016b49840f8c53bc1eb68a382e97b1482ecad7b148a6909a5c y = b2e0eaddfb84ccf9744464f82e160bfa9b8b64f9d4c03f999b8643f656b412a3
-
(Bloc 9 / Transaction 0 / Output 0 / scriptPubKey) Un octet indiquant si la clé est compressée ou non (en l'espèce, 0x04 indique qu'elle ne l'est pas) :
04
-
(Bloc 170 / Transaction 1 / Input 0 / scriptSig) Un octet indiquant le type du hash (en l'espèce, 0x01 correspond à SIGHASH_ALL) :
01
-
(Bloc 170 / Transaction 1 / Input 0 / scriptSig) Une signature :
304402204e45e16932b8af514961a1d3a1a25fdf3f4f7732e9d624c6c61548ab5fb8cd410220181522ec8eca07de4860a4acdd12909d831cc56cbbac4622082221a8768d1d09
Il s'agit d'une représentation sous forme de texte des valeurs hexadécimales des octets résultant l'encodage en DER (Distinguished Encoding Rules) de la structure ASN.1 (Abstract Syntax Notation One) d'une signature ECDSA (Elliptic Curve Digital Signature Algorithm). La structure ASN.1 est décrite dans la RFC 3279 :Ecdsa-Sig-Value ::= SEQUENCE { r INTEGER, s INTEGER }L'encodage d'une structure ASN.1 au format DER est décrit dans le standard X.690 :Identifiant3068 octets à suivre44Type entier02Longueur de l'entier (32 octets en big endian)20Valeur de l'entier (r)4e45e16932b8af514961a1d3a1a25fdf3f4f7732e9d624c6c61548ab5fb8cd41Type entier02Longueur de l'entier (32 octets en big endian)20Valeur de l'entier (s)181522ec8eca07de4860a4acdd12909d831cc56cbbac4622082221a8768d1d09Ces informations peuvent être récupérées en stockant les octets dans un fichier binaire, puis en utilisant OpenSSL :$ echo 304402204e45e16932b8af514961a1d3a1a25fdf3f4f7732e9d624c6c61548ab5fb8cd410220181522ec8eca07de4860a4acdd12909d831cc56cbbac4622082221a8768d1d09 > signature.txt $ xxd -r -p signature.txt signature.der $ openssl asn1parse -in signature.der -inform der 0:d=0 hl=2 l= 68 cons: SEQUENCE 2:d=1 hl=2 l= 32 prim: INTEGER :4E45E16932B8AF514961A1D3A1A25FDF3F4F7732E9D624C6C61548AB5FB8CD41 36:d=1 hl=2 l= 32 prim: INTEGER :181522EC8ECA07DE4860A4ACDD12909D831CC56CBBAC4622082221A8768D1D09
La transaction est une opération qui permet à son auteur de décrire un ensemble d'UTXO en entrée et un ensemble d'UTXO en sortie pour procéder à un transfert de BTC, modulo des frais dont il sera question plus tard. Le type de hash permet à l'auteur d'indiquer quelles inputs et ouputs il souhaite contraindre.
A vrai dire, cette possibilité, à laquelle il n'est pas fait recours en l'espèce car le type de hash est SIGHASH_ALL, semble assez théorique. Pour comprendre ce qu'il faut faire, le mieux est de se reporter au code de Bitcoin 0.1.0 et de dérouler ce qui se passe lors de la validation d'une signature.
Tout d'abord, il apparaît que la signature est une opération qui s'opère par input. Etant donné une transaction et une input, valider la signature pour une input consiste à :
- Faire une copie temporaire de la transaction 0 du bloc 170.
-
Modifier les inputs et ouputs de cette copie en fonction du type de hash :
SIGHASH_ALL Les inputs et les outputs ne sont pas modifiées SIGHASH_NONE Exception faite de l'input utilisée, la séquence de chaque input est passée à 0La liste des ouputs est vidéeSIGHASH_SINGLE Exception faite de l'input utilisée, la séquence de chaque input est passée à 0Toutes les outputs dont l'indice est strictement supérieur à celui de l'input utilisée sont suppriméesException faite de la dernière ouput, la valeur de toutes les outputs est passée à -1Exception faite de la dernière output, le scriptPubKey de toutes les outputs est vidéPar ailleurs, tout type de hash précédent peut être combiné à SIGHASH_ANYONECANPAY. Dans ce cas, exception faite de l'input utilisée, toutes les inputs sont supprimées. - Remplacer le scriptSig de l'input utilisée par le scriptPubKey de l'output qu'elle référence, c'est-à-dire l'output 0 de la transaction 0 du bloc 9.
-
Ecraser toute occurence de la signature tirée de scriptSig dans scriptPubKey avec des 0.Cette opération est précédée d'un commentaire "Drop the signature, since there's no way for a signature to sign itself", qui ne l'éclaire en rien. En effet, comment le scriptPubKey de l'output 0 de la transaction 0 du bloc 9 pourrait-il contenir ne serait-ce qu'une occurence de la signature figurant dans le scriptSig de l'input 0 de la transaction 1 du bloc 170, ce bloc n'ayant été généré qu'après ? Faut-il lire l'opération comme un rappel d'ordre général : qui veut faire figurer la signature du hash d'un document dans ce document, ne peut le faire figurer qu'à un endroit qui doit être écarté ou neutralisé, en étant rempli de 0 par exemple, lors du hashing ?Quelques recherches permettent de constater que certains se sont posés la question, mais que personne n'a vraiment apporté de réponse, comme :
- Sur ce forum : "It's legal to put a signature in the scriptPubKey -- Bitcoin just doesn't do so."
- Dans les commentaires de cette implémentation de Bitcoin en Python : "Of course, this can only come up in very contrived cases now that scriptSig and scriptPubKey are processed separately."
D'ailleurs cette étape n'est même plus mentionnée dans le schéma de la spécification.L'auteur de ces lignes a posé la question, et attend toujours une réponse... - Sérialiser la transaction, et y rajouter le type de hash sous la forme d'un entier sur 4 octets en little endian. Etant donné que le type de hash peut conduire à vider un script ou une liste d'inputs ou d'outputs, il n'est pas inutile de rappeler que ces données se présentent comme de tableaux qui sont sérialisés en précédant la sérialisation de leurs éléments de celle du nombre d'éléments en question. Ainsi, la sérialisation d'un script ou une liste vide se résume à un octet 0.
- Calculer le double SHA-256 en big endian de l'ensemble.
- Disposant du hash ainsi calculé, de la signature tirée de scriptSign de l'input 0 de la transaction 0 du bloc 170, et de la clé publique reconstituée à partir des valeurs de x et y tirée de scriptPubKey de l'output 0 de la transaction 0 du bloc 9, vérifier la signature.
Le programme validateTransaction.py dont le code figure dans l'archive qui accompagne cet article produit ainsi :
Signature: 304402204e45e16932b8af514961a1d3a1a25fdf3f4f7732e9d624c6c61548ab5fb8cd410220181522ec8eca07de4860a4acdd12909d831cc56cbbac4622082221a8768d1d09 Public key (x): 11db93e1dcdb8a016b49840f8c53bc1eb68a382e97b1482ecad7b148a6909a5c Public key (y): b2e0eaddfb84ccf9744464f82e160bfa9b8b64f9d4c03f999b8643f656b412a3 Hash: 7a05c6145f10101e9d6325494245adf1297d80f8f38d4d576d57cdba220bcb19
Pour vérifier la signature, ne passons pas par un module de Python, mais par OpenSSL, parce que c'est l'occasion d'en apprendre un peu sur le fonctionnement de couteau suisse de la crypto.
Pour commencer, il faut exporter la clé publique qui figure dans scriptPubKey sous la forme d'une structure ASN.1 au format DER. Cet exemple constitue un excellent point de départ.
La structure ASN.1 est spécifiée dans la RFC 5480 :
SubjectPublicKeyInfo ::= SEQUENCE {
algorithm AlgorithmIdentifier,
subjectPublicKey BIT STRING
}
AlgorithmIdentifier ::= SEQUENCE {
algorithm OBJECT IDENTIFIER,
parameters ANY DEFINED BY algorithm OPTIONAL
}
L'exemple cité plus tôt fournit toutes les informations requises pour transposer cette structure en au format DER. Toutefois, il est fait référence à une courbe qui n'est pas celle utilisée dans le Bitcoin : pour la clé publique il ne faut pas spécifier prime256v1, mais secp256k1.
Dans la structure, l'algorithme (ie : clé publique définie à l'aide d'une courbe elliptique) et son paramètre (ie : le type de courbe) sont identifiés à l'aide d'IOD (Object IDentifier) standardisés. Ces OID se présentent sous la forme d'une série de nombres séparés par des points, qui se code d'une manière particulière en binaire :
| ecPublicKey | 1.2.840.10045.2.1 | 06 07 2a 86 48 ce 3d 02 01 |
| secp256k1 | 1.3.132.0.10 | 06 05 2b 81 04 00 0a |
L'encodage est décrit ici. Qui veut s'épargner l'encodage doit chercher un peu le binaire sur le Web. Entre autres, on finit par trouver la séquence d'octets ici.
Au final, le binaire à générer est le suivant :
// SubjectPublicKeyInfo (0x56 octets) 30 56 // AlgorithmIdentifier (0x10 octets) 30 10 // AlgorithmIdentifier.algorithm 06 07 2a 86 48 ce 3d 02 01 // AlgorithmIdentifier.parameters 06 05 2b 81 04 00 0a // SubjectPublicKeyInfo.subjectPublicKey (0x42 octets) 03 42 00 // Clé non compressée 04 // x 11 db 93 e1 dc db 8a 01 6b 49 84 0f 8c 53 bc 1e b6 8a 38 2e 97 b1 48 2e ca d7 b1 48 a6 90 9a 5c // y b2 e0 ea dd fb 84 cc f9 74 44 64 f8 2e 16 0b fa 9b 8b 64 f9 d4 c0 3f 99 9b 86 43 f6 56 b4 12 a3
OpenSSL permet de vérifier que la clé publique est correctement générée. Il est possible de vérifier sa syntaxe ASN.1... :
$ openssl asn1parse -inform der -in public.der 0:d=0 hl=2 l= 86 cons: SEQUENCE 2:d=1 hl=2 l= 16 cons: SEQUENCE 4:d=2 hl=2 l= 7 prim: OBJECT :id-ecPublicKey 13:d=2 hl=2 l= 5 prim: OBJECT :secp256k1 20:d=1 hl=2 l= 66 prim: BIT STRING
...et son contenu :
$ openssl ec -pubin -inform der -in public.der -text -noout read EC key Public-Key: (256 bit) pub: 04:11:db:93:e1:dc:db:8a:01:6b:49:84:0f:8c:53: bc:1e:b6:8a:38:2e:97:b1:48:2e:ca:d7:b1:48:a6: 90:9a:5c:b2:e0:ea:dd:fb:84:cc:f9:74:44:64:f8: 2e:16:0b:fa:9b:8b:64:f9:d4:c0:3f:99:9b:86:43: f6:56:b4:12:a3 ASN1 OID: secp256k1
Accessoirement, la clé peut être convertie en PEM, qui n'est autre que sa représentation en base64 :
$ openssl ec -inform der -in public.der -outform pem -out public.pem
Ce qui donne donc :
-----BEGIN PUBLIC KEY----- MFYwEAYHKoZIzj0CAQYFK4EEAAoDQgAEEduT4dzbigFrSYQPjFO8HraKOC6XsUgu ytexSKaQmlyy4Ord+4TM+XREZPguFgv6m4tk+dTAP5mbhkP2VrQSow== -----END PUBLIC KEY-----
L'exportation de la signature au format DER ne pose pas de problème, car comme vu plus tôt, elle figure dans ce format dans scriptSig après l'opcode du PUSH.
Disposant du hash, de la clé publique et de la signature, tous en big endian, il est alors possible de vérifier la signature du hash à l'aide de la clé publique :
$ openssl pkeyutl -verify -pubin -inkey public.der -keyform der -sigfile signature.der -in hash.bin Signature Verified Succesfully
Ouf !
Vers l'infini, et au-delà
Si, pour bien s'approprier la manière dont la blockchain du Bitcoin est constituée, le développeur qui n'y connaît que pouic fourre son pif dans le code de la première version de Bitcoin et les échanges entre les larrons qui y ont contribué - pour autant que le farfelu à l'origine de tout ça se soit laissé influencer -, bref aux apparentes origines, notre bonhomme va tomber sur plus d'une ligne de C++ qui vont le laisser perplexe.
Ainsi, tout ce qui a été présenté plus tôt est parfaitement compréhensible, exception faite de la manière dont une transaction est signée. Enfin, techniquement, on comprend qu'il faille signer le hash d'un machin, mais c'est la nature du machin qui est pour le moins bizarre.
Sincèrement, c'est quoi ce bordel où je te fais des chichis sur le type de hash comme s'il pourrait y avoir du SIGHASH_ALL mais pas que, où je te copie le scriptPubKey de l'ouput de la transaction antérieure dans le scriptSig de l'input de la nouvelle, et comme si j'avais pas assez fait ma diva, où je t'écrase des occurrences de scriptSig dans scripPubKey, comme s'il pouvait en exister ?
A ce stade, il faut se garder d'un risque, qui est celui du moineton pris de vertige devant la Bible après avoir versé sans le savoir dans l'exégèse (toujours ?) abusive. Sans doute, notre développeur a encore des choses à comprendre qui ont une utilité, mais il y en a d'autres où vaut mieux pas qu'il cherche, car elles n'en ont probablement pas, soit qu'elles n'en ont jamais eue, soit qu'on a prétendu qu'elles pourraient en avoir, mais qu'elles n'en ont finalement jamais eue ou auxquelles on en a donné finalement une autre - sur le mode "C'est rigolo cet octet qui traîne dans un coin : je vais te l'utiliser pour faire un truc"...
Bref, tout ça pour dire que dans la tête du Nakamoto, les choses étaient peut-être claires, mais que dans son code, ça l'a été visiblement moins, et dans son article, je vous dis pas sur quoi il passe. Franchement, après avoir lu le code, les mecs qui pointent le papier comme si c'était les Saintes Evangiles me font doucement rigoler, car c'est un peu comme prétendre raconter un livre à partir du quatrième de couverture. Mais bon, on trouve des experts en la matière : Comment parler des livres que l'on n'a pas lus, si vous voulez un guide.
Bref, si vous voulez aller plus loin après ces investigations, je vous recommande de continuer sur votre lancée en passant à l'étude du code de Bitcoin Core, à l'appui de la lecture attentive des BIP - qui semblent fort bien rédigées. Pour ma part, je vais cesser de perdre du temps là-dessus : ça donne assez l'occasion aux spéculateurs et aux artistes à la con de défoncer futilement la planète pour qu'il soit nécessaire d'en rajouter.