Comment générer aléatoirement un labyrinthe à base de tunnels et de cavernes en creusant tant qu'il est possible un surface ? Le résultat doit ressembler à cette sorte de gruyère (la partie praticable est en gris) :
La solution
Creuser un labyrinthe est typiquement le genre de problème qui se résout en mettant en oeuvre des routines qui ne traitent pas le problème à la résolution duquel elles contribuent, mais une partie de ce dernier, en ignorant de plus le grand dessein auquel elles participent.
Ainsi, tout se passe comme si le labyrinthe était un résultat émergent, c'est-à-dire le produit d'actions individuelles d'acteurs qui n'ont pas de vision sur l'action collective à laquelle ils contribuent, action collective qui semble ne pas se réduire à la somme de leurs actions individuelles parce qu'elle semble régie par une logique distincte de celle qui anime les acteurs en question.
En l'espèce le labyrinthe peut être creusé en deux étapes qui s'ignorent, une première étape qui se saisit d'une carte quelconque et qui produit le réseau de tunnels et une seconde qui se saisit elle aussi d'une carte quelconque et qui produit des cavernes. De plus, chaque étape peut se résumer à une succession de décisions consistant à creuser un carré - ci-après, un "tile" - en fonction de l'état de ses voisins immédiats - creusé ou pas creusé. Tout comme les étapes, ces décisions s'ignorent : un décision est prise sans se soucier le moins du monde du fait que la succession des décisions à laquelle elle contribue finira par générer le résultat attendu.
Ainsi :
- Pour creuser le réseau de tunnels, il faut partir d'une carte remplie de tiles non-creusés et se positionner aléatoirement sur l'un d'entre eux. Après avoir creusé ce tile, il faut entreprendre de creuser les tiles voisins dans toutes les directions praticables parmi les quatre possibles : nord, ouest, sud et est. Une direction est praticable quand le tile voisin n'est pas lui-même voisin d'un tile déjà creusé. Le fonctionnement est récursif.
- Pour creuser les cavernes, il faut parcourir tous les tiles non-creusés pour en creuser certains. Ici, un tile doit être creusé s'il est au centre d'un certain motif composé de ses huit voisins dans les directions nord, nord-ouest, ouest, sud-ouest, sud, sud-est, est et nord-est. Ces motifs sont ceux où le tile constitue une sorte d'excroissance, c'est-à-dire quand il n'est pas solidaire de plus d'un voisin nord, ouest, sud ou est. Le fonctionnement est itératif.
Le code JavaScript
La carte est un simple tableau contenant des entiers
TILE_WALL si le tile est non-creusé, TILE_FLOOR si le tile est creusé. Le code pour creuser la carte est ventilé dans deux fonctions correspondant aux deux étapes citées à l'instant : carveTunnels () pour creuser les tunnels et carveRooms () pour creuser les cavernes.
carveTunnels () prend en entrée une référence sur le tableau d'entiers constituant la carte et les coordonnées à partir desquelles commencer à creuser. La carte est modifiée au fil d'appels récursifs :
function carveTunnels (map, x0, y0) {
var directions = [
{dx:0, dy:-1},
{dx:1, dy:-1},
{dx:1, dy:0},
{dx:1, dy:1},
{dx:0, dy:1},
{dx:-1, dy:1},
{dx:-1, dy:0},
{dx:-1, dy:-1}
];
var dStart, d, i, j, x1, y1, x2, y2, found;
map[x0 + y0 * g.mapWidth] = TILE_FLOOR;
dStart = randomInt (0, 3) << 1;
d = dStart;
while (true) {
x1 = x0 + directions[d].dx;
y1 = y0 + directions[d].dy;
if ((x1 >= 0) && (x1 < g.mapWidth) && (y1 >= 0) && (y1 < g.mapHeight)) {
i = x1 + y1 * g.mapWidth;
if (map[i] == TILE_WALL) {
found = true;
for (j = 0; j != 8; j ++) {
if (j == ((d + 4) % 8))
continue;
if (j == ((d + 3) % 8))
continue;
if (j == ((d + 5) % 8))
continue;
x2 = x1 + directions[j].dx;
y2 = y1 + directions[j].dy;
if ((x2 < 0) || (x2 == g.mapWidth) || (y2 < 0) || (y2 == g.mapHeight))
continue;
if (map[x2 + y2 * g.mapWidth] != TILE_WALL) {
found = false;
break;
}
}
if (found) {
map[x1 + y1 * g.mapWidth] = TILE_CARVING;
this.carveTunnels (map, x1, y1);
}
}
}
d += 2;
if (d == 8)
d = 0;
if (d == dStart)
break;
}
}
carveRooms () prend en entrée une référence sur le tableau d'entiers uniquement. La carte est modifiée au fil d'appels itératifs :
function carveRooms (map) {
var directions = [
{dx:-1, dy:-1},
{dx:0, dy:-1},
{dx:1, dy:-1},
{dx:1, dy:0},
{dx:1, dy:1},
{dx:0, dy:1},
{dx:-1, dy:1},
{dx:-1, dy:0}
];
var x0, y0, x1, y1, i, j, nbCarvedTiles, found;
var pattern = new Array (8);
var patterns = [
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1],
[1, 1, 1, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 1, 0, 0, 0],
[0, 0, 0, 0, 1, 1, 1, 0],
[1, 0, 0, 0, 0, 0, 1, 1],
[1, 1, 0, 0, 0, 0, 0, 1],
[0, 1, 1, 1, 0, 0, 0, 0],
[0, 0, 0, 1, 1, 1, 0, 0],
[0, 0, 0, 0, 0, 1, 1, 1],
[1, 1, 1, 0, 0, 0, 0, 1],
[0, 1, 1, 1, 1, 0, 0, 0],
[0, 0, 0, 1, 1, 1, 1, 0],
[1, 0, 0, 0, 0, 1, 1, 1],
[1, 1, 0, 0, 0, 0, 1, 1],
[1, 1, 1, 1, 0, 0, 0, 0],
[0, 0, 1, 1, 1, 1, 0, 0],
[0, 0, 0, 0, 1, 1, 1, 1],
[1, 1, 1, 0, 0, 0, 1, 1],
[1, 1, 1, 1, 1, 0, 0, 0],
[0, 0, 1, 1, 1, 1, 1, 0],
[1, 0, 0, 0, 1, 1, 1, 1],
[1, 1, 1, 1, 0, 0, 1, 1],
[1, 1, 1, 1, 1, 1, 0, 0],
[0, 0, 1, 1, 1, 1, 1, 1],
[1, 1, 0, 0, 1, 1, 1, 1],
[1, 1, 1, 0, 0, 1, 1, 1],
[1, 1, 1, 1, 1, 0, 0, 1],
[0, 1, 1, 1, 1, 1, 1, 0],
[1, 0, 0, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 0, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 0],
[1, 0, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 0, 1, 1, 1, 1]
];
do {
nbCarvedTiles = 0;
for (y0 = 0; y0 != g.mapHeight; y0 ++) {
for (x0 = 0; x0 != g.mapWidth; x0 ++) {
if (map[x0 + y0 * g.mapWidth] == TILE_FLOOR)
continue;
for (i = 0; i != 8; i ++) {
pattern[i] = 0;
x1 = x0 + directions[i].dx;
y1 = y0 + directions[i].dy;
if ((x1 < 0) || (x1 == g.mapWidth) || (y1 < 0) || (y1 == g.mapHeight))
continue;
if (map[x1 + y1 * g.mapWidth] == TILE_WALL)
pattern[i] = 1;
}
for (i = 0; i != patterns.length; i ++) {
found = true;
for (j = 0; j != 8; j ++) {
if (patterns[i][j] != pattern[j]) {
found = false;
break;
}
}
if (found) {
map[x0 + y0 * g.mapWidth] = TILE_FLOOR;
nbCarvedTiles ++;
break;
}
}
}
}
} while (nbCarvedTiles);
}
L'exemple
Cliquez ici pour accéder à une page de test minimaliste. Vous pourrez visualiser le code et le récupérer pour travailler avec.
La logique
Creuser les tunnels
En fait de tunnels, il faut plutôt parler de tunnel, car c'est un seul tunnel qui est creusé, en s'assurant de plus que tous les tiles qu'il est possible de creuser sont creusés.
Le point de départ est un tile non-creusé de coordonnées aléatoires. Après l'avoir creusé, il s'agit de passer en revue tous ses voisins qui ne sont pas encore creusés pour déterminer s'ils peuvent être creusés à leur tour.
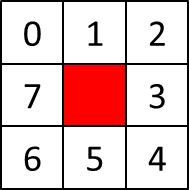
Afin de s'éviter des tests à répétition pour déterminer les incréments à utiliser en abscisse comme en ordonnée pour progresser dans la carte, une indexation des directions est mise en place :
De la sorte, il est simple d'indexer les incréments dans un tableau qui les regroupe :
var directions = [
{dx:-1, dy:-1},
{dx:0, dy:-1},
{dx:1, dy:-1},
{dx:1, dy:0},
{dx:1, dy:1},
{dx:0, dy:1},
{dx:-1, dy:1},
{dx:-1, dy:0}
];
L'objectif étant de générer un labyrinthe à base de murs droits (horizontaux ou verticaux), les tiles voisins candidats pour être creusés sont ceux situés au nord, à l'est, au sud et à l'ouest du tile courant.
Toutefois, un tile voisin ne peut être creusé que sous trois conditions :
- il existe, c'est-à-dire qu'il est dans les limites de la carte ;
- il n'est pas déjà creusé, car il s'agit d'éviter de rebrousser chemin à l'infini ;
- il n'est pas voisin de tiles déjà creusés, car il s'agit de creuser un tunnel et un seul.
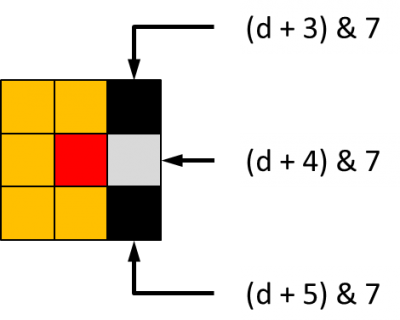
Pour s'assurer que la troisième condition est vérifiée, il faut donc tester les voisins du tile voisin candidat. Le cas de figure qui se présente est récurrent. Le tile courant est en gris, le tile voisin candidat est en rouge, les tiles voisins de ce dernier sont en orange. Si jamais un tile orange est creusé, le tile rouge ne peut pas être creusé.
Si
d est la direction par laquelle on passe du tile courant au tile voisin candidat, alors les tiles voisins de ce voisin qu'il faut contrôler sont dans toutes les directions exception faite de :
-
(d + 4) & 7 -
(d + 3) & 7 -
(d + 5) & 7
En effet, calculer
(d + n) & 7 revient à calculer (d + n) % 8. En masquant par 7 pour ne retenir que les trois derniers bits, on retient le reste de la division entière par 8, ce qui évite d'avoir à procéder à cette dernière via l'opérateur modulo (%). Manoeuvre datée pour économiser un division, mais on ne sait jamais : en matière d'optimisation, les petits ruisseaux font les grandes rivières...
Pour résumer, si (
x0, y0) désigne le tile courant, les tiles voisins se trouvent dans chacune des quatre directions horizontales et verticales parcourues à partir de l'une d'entre elles choisie au hasard :
dStart = randomInt (0, 3) << 1; d = dStart;
Tant qu'il est possible de creuser, il s'agit alors de déterminer les coordonnées du tile voisin courant (
x1, y1) :
x1 = x0 + directions[d].dx; y1 = y0 + directions[d].dy;
Pour déterminer si ce tile voisin peut être creusé, il faut déjà s'assurer qu'il se trouve dans la carte :
if ((x1 >= 0) && (x1 < g.mapWidth) && (y1 >= 0) && (y1 < g.mapHeight)) {
//...
}
Ensuite, il faut s'assurer qu'il n'est pas déjà creusé :
i = x1 + y1 * g.mapWidth;
if (map[i] == TILE_WALL) {
//...
}
Enfin, il faut vérifier qu'aucun de ses voisins (
x2, y2), pour autant qu'il existe, n'est déjà creusé :
found = true;
for (j = 0; j != 8; j ++) {
if (j == ((d + 4) & 7))
continue;
if (j == ((d + 3) & 7))
continue;
if (j == ((d + 5) & 7))
continue;
x2 = x1 + directions[j].dx;
y2 = y1 + directions[j].dy;
if ((x2 < 0) || (x2 == g.mapWidth) || (y2 < 0) || (y2 == g.mapHeight))
continue;
if (map[x2 + y2 * g.mapWidth] != TILE_WALL) {
found = false;
break;
}
}
Si le tile voisin peut être creusé, alors il est creusé et le travail se poursuit en appelant récursivement
carveTunnels () :
if (found) {
map[x1 + y1 * g.mapWidth] = TILE_CARVING;
this.carveTunnels (map, x1, y1);
}
La petite subtilité consiste à marquer le tile voisin mais à ne pas le creuser tout de suite, car la première opération accomplie par
carveTunnels () consiste justement à le creuser. De la sorte, il n'est pas creusé deux fois. Cela importe peu dans cet exemple où creuser un tile se résume à modifier la valeur d'un entier dans un tableau, mais cela pourrait importer dans d'autres contextes où creuser un tile engage des opérations plus lourdes.
Creuser les cavernes
Pour creuser les cavernes, nul besoin d'élaborer un algorithme compliqué qui identifie ce qu'est une caverne. Tout commme
carveTunnels () n'a aucune notion du tunnel qu'elle creuse, carveRooms () n'a aucune notion des cavernes qu'elle creuse : ces fonctions ne voient qu'une chose, le tile courant qu'elle doivent creuser si jamais il répond à certaines conditions.
La contemplation d'une carte creusée par
carveTunnels () donne rapidement une idée de ce qu'il serait possible de faire pour creuser des cavernes. Il s'agirait de creuser des tiles qui constituent des excroissances (les tiles en gris recolorés en rouge) :
Une liste des motifs dont les tiles concernés constituent le centre peut être dressée :
Le traitement consiste à parcourir la carte tile par tile et à tester si le tile est au centre d'un de ces motifs :
for (y0 = 0; y0 != g.mapHeight; y0 ++) {
for (x0 = 0; x0 != g.mapWidth; x0 ++) {
// ...
}
}
Tout d'abord, le tile ne doit donc pas avoir été creusé :
if (map[x0 + y0 * g.mapWidth] == TILE_FLOOR) continue;
Ensuite, le tile doit être au centre d'un des motifs recensés. Pour le savoir, le motif dont le tile occupe le centre est reconstitué en sondant ses huits voisins, dans la limite de ceux qui existent (ie : qui sont dans les limites de la carte) :
for (i = 0; i != 8; i ++) {
pattern[i] = 0;
x1 = x0 + directions[i].dx;
y1 = y0 + directions[i].dy;
if ((x1 < 0) || (x1 == g.mapWidth) || (y1 < 0) || (y1 == g.mapHeight))
continue;
if (map[x1 + y1 * g.mapWidth] == TILE_WALL)
pattern[i] = 1;
}
Le motif établi, il est comparé à tous ceux qui sont recensés jusqu'à ce qu'un motif corresponde ou qu'aucun ne corresponde. Si un motif correspond, le tile est creusé :
for (i = 0; i != patterns.length; i ++) {
found = true;
for (j = 0; j != 8; j ++) {
if (patterns[i][j] != pattern[j]) {
found = false;
break;
}
}
if (found) {
map[x0 + y0 * g.mapWidth] = TILE_FLOOR;
nbCarvedTiles ++;
break;
}
}
Nul doute qu'il serait possible d'optimiser un peu en trouvant des associations entre les motifs afin d'en éliminer par paquet sur un seul test...
Enfin, ce parcours de l'intégralité des tiles de la carte est répété tant qu'il se trouve des tiles à creuser. En effet, creuser un tile modifie le motif dont ses voisins non-creusés sont les centres. Toutefois, seuls les voisins qui n'ont pas encore été parcourus seront traités ; pour les voisins déjà parcourus, il faut organiser un nouveau parcours. Tout le code d'un parcours est donc placé au sein d'une boucle :
do {
nbCarvedTiles = 0;
// ...
} while (nbCarvedTiles);
Si son nombre d'itérations est incertain, l'issue de cette boucle est certaine, car au pire il ne restera plus aucun tile à creuser. Voici ce que donne l'avant et l'après :
Le labyrinthe généré ici présente la particularité que les murs sont toujours droits (horizontaux ou verticaux). Il est possible de relâcher la contrainte pour que les murs soient aussi diagonaux, comme sur cet exemple (la partie praticable est en gris) :
Toutefois, l'intérêt de creuser des murs droits est de produire des angles toujours composés de trois tiles non-creusés. Cela s'avère utile pour faciliter certains calculs, comme l'interception de rayons émis depuis un tile pour déterminer les tiles visibles depuis ce dernier. En effet, si un angle n'est composé que deux tiles non-creusés, un rayon peut fort bien passer entre les deux et offrir une vision sur des tiles qui sont en fait de l'autre côté du mur...
Cliquez ici pour accéder à une page de test minimaliste. Vous pourrez visualiser le code et le récupérer pour travailler avec.