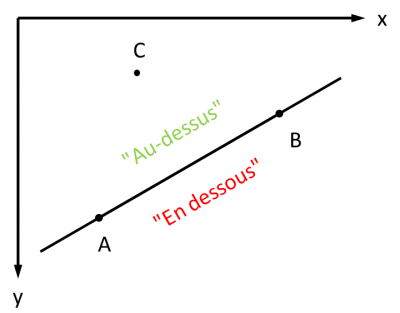
Comment déterminer si un point se trouve "au-dessus" ou "en dessous" d'une droite ?
La solution
La position d'un point M par rapport à une droite AB (orientée de A vers B) se détermine en étudiant le produit vectoriel des vecteurs AB et AM.
Le code JavaScript
En JavaScript, la solution se traduit par le code suivant :
- /*------------------------------------------------------------------------------
- Retourne le produit vectoriel non normalisé (repère X de gauche à droite, Y du
- haut vers le bas).
- ENTREE :
- v0 Vecteur AB (v0.x = xB - xA et v0.y = yB - yA)
- v1 Vecteur CD (v1.x = xD - xC et v1.y = yD - yC)
- SORTIE :
- Produit vectoriel non normalisé :
- < 0 si l'angle de AB à CD est dans ]PI/2, 3*PI/2[
- = 0 si AB est orthogonal à CD
- > 0 si l'angle de AB à CD est dans ]3*PI/2, PI/2[
- ------------------------------------------------------------------------------*/
- function crossProduct (v0, v1) {
- return ((v0.y * v1.x) - (v0.x * v1.y));
- }
La position relative du point M par rapport à la droite AB le fruit d'une interprétation arbitraire du signe du produit vectoriel dans un contexte défini par l'orientation des axes et le sens de rotation. Par exemple :
- var A = {x:100, y:300};
- var B = {x:300, y:100};
- var M = {x:150, y:100};
- var AB = {x:(B.x - A.x), y:(B.y - A.y)};
- var AM = {x:(M.x - A.x), y:(M.y - A.y)};
- var cp = crossProduct (AB.x, AB.y, AM.x, AM.y);
- if (!cp)
- window.alert ("AB et AM parallèles");
- else {
- if (cp > 0)
- window.alert ("M au-dessus de AB");
- else
- window.alert ("M en dessous de AB");
- }
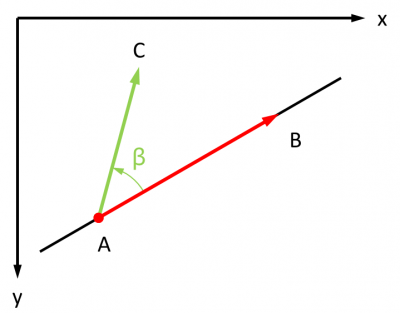
Ainsi, il est parfaitement possible de poser que M doit être considéré comme "au-dessus" de AB quand l'angle formé par les vecteurs AB et AM (M étant l'image de B par une rotation de centre A dans le sens trigonométrique dans un repère dont l'axe des abscisses est orienté de gauche à droite et l'axe des ordonnées de haut en bas) est dans ]0, PI[, donc quand le produit vectoriel des vecteurs AB et AM est positif. Dans ce même contexte, ou pourrait tout aussi bien décider que c'est quand ce produit vectoriel est négatif. Tout dépend de l'objectif poursuivi.
L'exemple
Cliquez ici pour accéder à une page de test minimaliste qui utilise SVG. Vous pourrez visualiser le code et le récupérer pour travailler avec.
Les maths
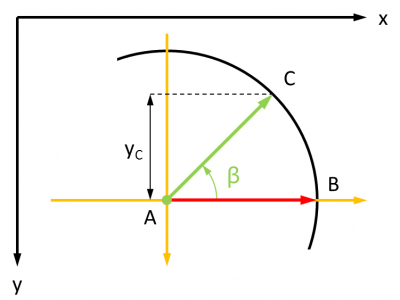
Considérons un instant que AB soit horizontale, et que B et C se trouvent sur un cercle trigonométrique de centre A. Dans ce cas, C se trouve "au dessus" de AB lorsque son ordonnée yC est négative dans le repère d'origine A (représentée en jaune) et "en-dessous" quand cette ordonnée est positive dans ce même repère.
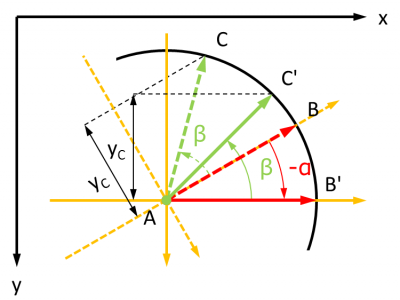
C'est donc le signe de sin (β) dans le repère d'origine A et dont l'axe des abscisses est AB qu'il faut étudier. Dans le cas général, AB est orientée d'un angle α quelconque dans le repère de l'écran.
Dans ces conditions, calculer yC dans le repère de centre A et d'axe des abscisses AB revient à calculer les coordonnées de l'image de C par une rotation de -α dans le repère de centre A et d'axe des abscisses AM, horizontal. A la base, les coordonnées de C dans le premier repère sont :
- xC - xA
- yC - yA
Si on applique la rotation comme expliqué ici, les coordonnées de C deviennent :
- (xC - xA) * cos (-α) + (yC - yA) * sin (-α)
- - (xC - xA) * sin (-α) + (yC - yA) * cos (-α)
Et comme cos (-α) = cos (α) et sin (-α) = -sin(α) :
- (xC - xA) * cos (α) - (yC - yA) * sin (α)
- (xC - xA) * sin (α) + (yC - yA) * cos (α)
Mais on sait que :
- xB = AB * cos (α) + xA
- yB = - AB * sin (α) + yA
C'est-à-dire que :
- cos (α) = (xB - xA) / AB
- sin (α) = - (yB - yA) / AB
Donc, en remplaçant cos (α) et sin (α), les coordonnées de C au terme de la rotation s'écrivent :
- ((xC - xA) * (xB - xA) + (yC - yA) * (yB - yA)) / AB
- (- (xC - xA) * (yB - yA) + (yC - yA) * (xB - xA)) / AB
Comme AB est toujours positif, le signe de yC est bien donné par (xB - xA) * (yC - yA) - (xC - xA) * (yB - yA), c'est-à-dire par le produit vectoriel des vecteurs AB et AC.