La multiplication des coordonnées

(Xe, Ye, Ze, 1.0)

d'un point par la matrice de projection de WebGL produit des coordonnées de clipping

(Xc, Yc, Zc, Wc)

Comment en déduire les coordonnées du pixel

(Xs, Ys)

dans le canvas ? A l'inverse, comment retrouver les coordonnées du point à partir des coordonnées du pixel ?

Reportez-vous à cet article pour comprendre comment former la matrice de projection de WebGL.

La projection

La multiplication des coordonnées

(Xe, Ye, Ze, 1.0)

d'un point dans l'espace produit les coordonnées de clipping

(Xc, Yc, Zc, Wc)

. La question est : comment passer de

(Xc, Yc, Zc, Wc)

aux coordonnées

(Xs, Ys)

d'un pixel dans la surface de projection de dimensions

width

par

height

à l'écran ?

On sait qu'il faut diviser les coordonnées de clipping

(Xc, Yc, Zc, Wc)

par

Wc

pour trouver les coordonnées de projection

(Xp = \frac{Xc}{Wc}, Yp = \frac{Yc}{Wc}, Zp = \frac{Zc}{Wc}, 1.0)

, et que c'est à partir de ces dernières coordonnées qu'il est possible de trouver

(Xs, Ys)

Reste à savoir comment.

Pour passer de

(Xp, Yp, Zp, 1.0)

(Xs, Ys)

, il faut considérer :

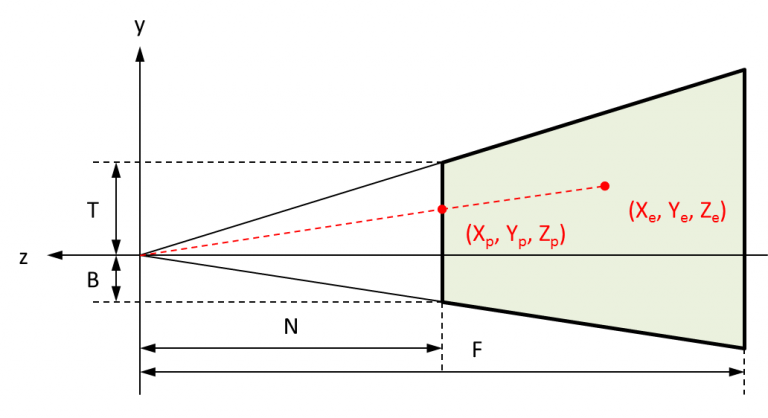
que $(Xp, Yp)$ sont données dans une surface de $2.0$ par $2.0$ qui correspond directement à la surface de projection de $width$ par $height$ (NB : la prise en compte des aspect ratios dans la matrice de projection fait que cette correspondance est directe). En effet, le volume de clipping s'étend de $(-1.0, -1.0, -1.0)$ à $(1.0, 1.0, 1.0)$ , si bien que chacune de ses faces fait $2.0$ par $2.0$ , notamment la face avant qui sert de surface de projection ;
que l'axe des ordonnées à l'écran est inversé par rapport à l'axe des ordonnées dans l'espace.

Par conséquent :

xp = xc / wc
yp = yc / wc
zp = zc / wc
wp = wc / wc

Finalement :

xs = (xp + 1.0) * width / 2.0
ys = (1.0 - yp) * height / 2.0

La rétroprojection

Le problème est donc l'inverse : retrouver les coordonnées

(Xe, Ye, Ze, 1.0)

du point qui correspond au pixel en

(Xs, Ys)

sur la surface de projection de dimensions

width

par

height

à l'écran.

Pour commencer, il faut retrouver les coordonnées de la projection

(Xp, Yp, Zp, 1.0)

. Ce sont des coordonnées normalisées, c'est-à-dire comprises entre

-1.0

1.0

$Xp$ et $Yp$ sont exprimées dans le repère de la face avant du volume de clipping. Les dimensions de cette face sont $2.0$ par $2.0$ . Si pour simplifier on pose que $left = -right$ et $top = -bottom$ , l'origine de son repère se trouve au centre de la face. Enfin, la face correspond directement à la surface de projection de $width$ par $height$ , du fait de la prise en compte des aspect ratios dans la matrice de projection.
$Zp$ correspond à la version normalisée de la profondeur de cette face, soit $-1.0$ .