Pas d'application en 3D interactive sans ray casting ! Cette technique permet de calculer les coordonnées du point d'une surface 3D dont un pixel est la représentation de la projection. Le ray casting sert de base au ray picking, qui permet de déterminer quelle est la surface 3D en question parmi toutes celles de tous les objets 3D de la scène 3D projetée.
Le ray casting constitue une étape importante dans la progression de la connaissance du développeur qui se lance dans la 3D. En effet, l'implémenter correctement suppose d'avoir les idées claires sur le pipeline de transformation.
Explications à l'appui d'un exemple dans ce qui suit.
Avertissements
Cliquez ici pour tester l'exemple, et là pour récupérer une archive contenant tout le code correspondant pour travailler avec.
Cet article se focalise sur le ray casting, et l'exemple ne sert vraiment qu'à illustrer. Par conséquent, il n'est pas question de passer ce dernier en revue pour expliquer comment le rendu d'une scène 3D est assuré au moyen d'un ensemble d'objets de base que sont Renderer, Scene et autres : ce sera pour un autre article.
La seule chose qu'il faut savoir, c'est que l'exemple mobilise une bibliothèque maison pour tout ce qui concerne la manipulation de vecteurs et de matrices : libWEBGL.js.
Cette bibliothèque se présente sous la forme d'un objet libWEBGL dont la déclaration est importée dans le programme qui l'utilise. L'objet contient des méthodes, destinées à être appelées directement pour réaliser une tâche ou pour créer un objet - des fabriques. En l'espèce, l'objet libWEBGL ne contient que des fabriques :
- var libWEBGL = {
- createVSHelper: function (gl) {
- return (new this.VertexShaderHelper (gl));
- },
- createFSHelper: function (gl) {
- return (new this.FragmentShaderHelper (gl));
- },
- createMatrix2D: function (m) {
- return (new this.Matrix2D (m));
- },
- createVector2D: function (v) {
- return (new this.Vector2D (v));
- },
- createMatrix3D: function (m) {
- return (new this.Matrix3D (m));
- },
- createVector3D: function (v) {
- return (new this.Vector3D (v));
- }
- };
Plus loin dans le code de libWEBGL.js, on trouve la déclaration des constructeurs des objets appelés par les fabriques, et tout ce que ces objets contiennent. Par exemple, pour Vector3D :
- // Le constructeur
- libWEBGL.Vector3D = function (v) {
- this.v = new Array (4);
- if (v === undefined)
- this.origin ();
- else
- this.load (v);
- };
- // Une méthode .load ()
- libWEBGL.Vector3D.prototype.load = function (v) {
- var i;
- for (i = 0; i !== 4; i ++)
- this.v[i] = v[i];
- return (this);
- };
- // Une propriété .x pour le coup définie avec des accesseurs
- Object.defineProperty (libWEBGL.Vector3D.prototype, "x", {
- get: function () { return (this.v[0]); },
- set: function (x) { this.v[0] = x; }
- });
- // Etc.
L'exemple donné ici n'utilise que les objets libWEBGL.Vector3D et libWEBGL.Matrix3D, qui représentent un vecteur 4x1 et une matrice 4x4, respectivement. Pour en savoir plus sur la manière dont ces objets implémentent des opérations mathématiques, tout particulièrement la multiplication, référez-vous aux abondants commentaires dans libWEBGL.js.
Petit rappel sur le pipeline de transformation
Dans un moteur 3D, tout point de l'espace subit une séquence de transformations qui sont codées dans des matrices 4x4 :
- des transformations dans le repère de l'objet auquel il appartient via une matrice locale mL ;
- des transformations dans le repère de la scène via une matrice du monde mW ;
- des transformations dans le repère de la vue via une matrice mV ;
- une projection via une matrice mP.
Dans l'exemple :
- la matrice locale de chaque objet 3D est une matrice identité ;
- la matrice du monde sert à appliquer à tous les objets 3D de la scène une rotation de 45° autour de l'axe des abscisses, puis une rotation de 45° autour de l'axe des affixes ;
- la matrice de la vue sert à appliquer à tous les objets de la scène ainsi transformés une translation le long de l'axe des affixes, pour placer tout cela à bonne distance de l'observateur ;
- la matrice de projection est conforme au modèle longuement expliqué dans cet article.
Un point important pour bien lire les opérations matricielles qui vont suivre, c'est que WebGL utilise des vecteurs et des matrices en colonne, ce qui implique que dans le code d'un shader, la séquence de transformation que subit un point s'écrit ainsi :
mP * mV * mW * mL * v
Toutefois, dans ce qui suit, pour des raisons qui sont extensivement expliquées dans les commentaires figurant dans libWEBGL.js, les vecteurs et les matrices sont en ligne, ce qui implique que la même séquence s'écrit ainsi :
v * mL * mW * mV * mP
Entre autres, c'est franchement plus intuitif, car l'ordre des transformations est celui de la lecture, de gauche à droite.
La composition de la scène
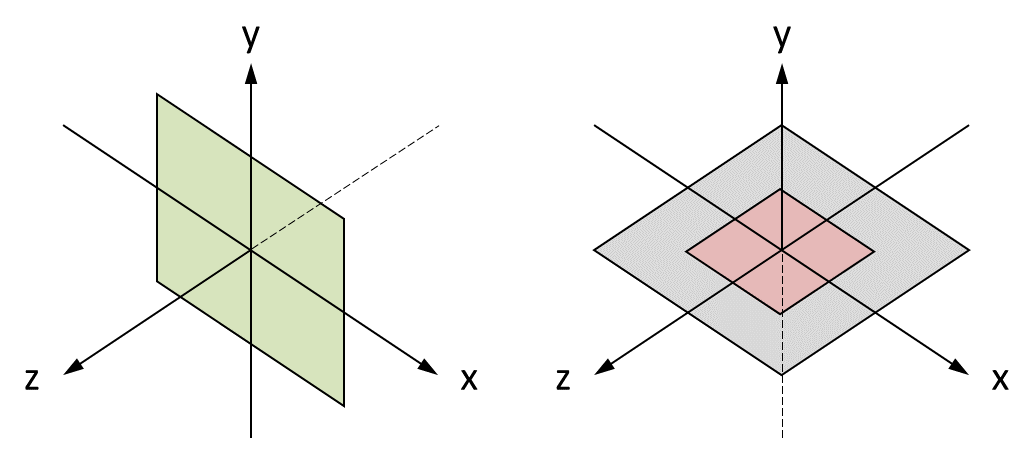
Dans l'exemple, vous contemplez une scène composée d'objets 3D qui ont subi les transformations décrites à l'instant. Elle comprend une surface grise inclinée. Si vous déplacez dessus le pointeur de la souris, deux autres surfaces accompagnent le mouvement :
- Une surface verte, qui apparaît dans le plan de la face de devant du volume de clipping, c'est-à-dire dans le plan de la surface de projection. Cette surface verte est centrée sur le point dont le pixel est la représentation dans le canvas - le canvas n'est que la représentation à l'écran de la surface de projection.
- Une surface rouge, qui apparaît dans le plan de la surface grise. Cette surface est centrée sur le point d'intersection entre le rayon qui part de l'oeil de l'observateur, c'est-à-dire l'origine du repère de la vue, et qui passe par le point précédemment évoqué de la surface de projection, et la surface grise.
A la base, toutes ces surfaces sont définies dans le repère de la scène, centrées sur l'origine de ce dernier. Les surfaces grise et rouge sont définies dans le plan ZX, tandis que la surface verte est définie dans le plan XY.
Un travail en quatre étapes
Pour parvenir au résultat, la première étape consiste à calculer les coordonnées du point P, projection inverse du pixel survolé. C'est un point de la surface de projection dont les coordonnées sont exprimées dans le repère de la vue. Le détail du calcul a été présenté cet article. Cela donne :
- r = this.wglContext.tag.getBoundingClientRect ();
- x = e.clientX - Math.round (r.left);
- y = e.clientY - Math.round (r.top);
- projectionPoint = libWEBGL.createVector3D ([
- -NEAR * (x / (this.wglContext.width / 2.0) - 1.0),
- -NEAR * (1.0 - y / (this.wglContext.height / 2.0)),
- NEAR * 1.0,
- -NEAR
- ]);
- m = this.scene.renderer.getMatrixP ();
- m.inverse ();
- projectionPoint.transform (m);
La deuxième étape consiste à appliquer à la surface verte, définie dans le plan XY du repère de la scène, les transformations inverses à celles que le pipeline de transformation va lui faire subir, pour annuler par anticipation les effets de ces dernières. De ce fait, lors du rendu, tout va se passer comme si la surface verte avait été définie dans le plan de la surface de projection dans le repère de la vue. Partant, pour centrer cette surface sur le point P, il suffit de redéfinir sa matrice locale pour lui appliquer une translation aux coordonnées du point P :
- mW = this.scene.renderer.getMatrixW ();
- mW.inverse ();
- mV = this.scene.renderer.getMatrixV ();
- mV.inverse ();
- mL = libWEBGL.createMatrix3D ();
- mL.setTranslation (projectionPoint.x, projectionPoint.y, projectionPoint.z - EPSILON);
- mL.multiply (mV, mW);
- this.scene.pointXY.matrix.copy (mL);
Le recours à EPSILON est expliqué plus loin.
La troisième étape consiste à calculer l'intersection I du rayon qui part de l'oeil de l'observateur - l'origine du repère de la vue - et qui passe par le point P, avec le plan de la surface grise. Comme les coordonnées de P sont exprimées dans le repère de la vue, il faut rapporter les coordonnées des éléments qui définissent le plan - un point et un vecteur normal - dans ce même repère, ce qui implique de simuler leur transformation par le pipeline jusqu'à la projection exclue :
- r0 = libWEBGL.createVector3D ([0.0, 0.0, 0.0, 1.0]); // Origine du rayon
- r1 = projectionPoint; // Point sur la surface de projection par lequel passe le rayon
- n0 = libWEBGL.createVector3D ([0.0, 0.0, 0.0, 1.0]); // Origine de la normale au plan
- n1 = libWEBGL.createVector3D ([0.0, 1.0, 0.0, 1.0]); // Fin de la normale au plan
- p = libWEBGL.createVector3D ([0.0, 0.0, 0.0, 1.0]); // Point quelconque sur le plan (ie : x et z quelconques, mais y est l'ordonnée du plan)
- mW = this.scene.renderer.getMatrixW ();
- mV = this.scene.renderer.getMatrixV ();
- n0.transform (mW, mV);
- n1.transform (mW, mV);
- n = n1.clone ();
- n.sub (n0);
- p.transform (mW, mV);
Pour ce qui concerne le calcul de l'intersection, cela ne s'invente pas. Le code est une implémentation de cet algorithme d'un certain Badouel :
- w = r0.clone ();
- w.sub (p);
- u = r1.clone ();
- u.sub (r0);
- s = -n.dot (w) / n.dot (u);
- u.scale (s);
- intersectionPoint = r0.clone ();
- intersectionPoint.add (u);
La quatrième et dernière étape consiste à appliquer les transformations inverses au point I, dont les coordonnées viennent d'être calculées dans le repère de la vue, pour rapporter ces dernières dans le repère de la scène. En effet, il faut centrer la surface rouge sur le point I. Or tout comme la surface grise, cette surface est définie dans le plan ZX de la scène, et ses coordonnées sont donc exprimées dans le repère de cette dernière. Un fois que le point I a été rapporté dans ce repère, il suffit de redéfinir la matrice locale de la surface rouge pour lui appliquer une translation aux coordonnées du point I :
- mW.inverse ();
- mV.inverse ();
- intersectionPoint.transform (mV, mW);
- mL = libWEBGL.createMatrix3D ();
- mL.setTranslation (intersectionPoint.x, intersectionPoint.y + EPSILON, intersectionPoint.z);
- this.scene.pointZX.matrix.copy (mL);
Eviter le combat de Z
Pour l'anecdote, c'est quoi EPSILON ?
Selon l'ordre de grandeur des profondeurs et la précision des calculs, il se peut que positionner la surface verte à la profondeur exacte de la surface de projection conduise à l'élimination totale ou partielle de cette dernière par z-fighting ou clipping.
Pour l'éviter, il suffit de reculer la surface rouge par rapport à la surface de projection, d'une valeur arbitraire aussi infinitésimale que possible au regard de l'ordre de grandeur pour éviter d'introduire une déformation perceptible au rendu. Ces surfaces étant définies dans le plan XY du repère de la vue, cela revient à retrancher une valeur EPSILON empiriquement fixée à 0.00001 à l'affixe de la surface verte.
Le même problème survient entre la surface rouge et la surface grise, puisque la première est censée se trouver dans le plan de la seconde. Une solution du même ordre s'applique. Puisque ces surfaces sont définies dans le plan ZX du repère de la scène, il s'agit de décaler légèrement la surface rouge par rapport à la surface grise le long de l'axe des ordonnées. Noter que dans l'exemple, la surface rouge est ainsi surélevée par rapport à la surface grise, mais tout dépend de l'angle sous lequel la scène est observée...